
|
|
Метод индуктивно связанных контуров
| |
| FedinMA | Дата: Четверг, 02.10.2008, 21:54 | Сообщение # 1 |
 Асс. каф. ФЭМАЭК
Группа: Модераторы
Сообщений: 227
Статус: Offline
| Влад, посмотри почту. Это последняя версия перед переходом к Model. Сюда, наверное, выкладывать весь код бессмысленно, да и проблематично.
Модуль метода связанных контуров - 18. Если будут проблемы со стеком, то придется увеличивать в процедуре создания формы, т.к. у меня не динамические массивы.
Учиться надо так, чтобы это было тебе в радость.
|
| |
| |
| DEADalus | Дата: Четверг, 02.10.2008, 21:56 | Сообщение # 2 |
 Админище
Группа: Администраторы
Сообщений: 98
Статус: Offline
| Грасиас
Свобода - это когда ты одинок, молод и безвестен.
(Фредерик Бегбедер "Windows on the World")

|
| |
| |
| FedinMA | Дата: Воскресенье, 12.10.2008, 17:38 | Сообщение # 3 |
 Асс. каф. ФЭМАЭК
Группа: Модераторы
Сообщений: 227
Статус: Offline
| Чтобы легче было разобраться в коде, добрался до своих бумажных архивов)
Итак, рассмотрим следующий случай:
Число витков индуктора w=2
Число разбиений каждого витка - 2 (ni*nj)
Число разбиений загрузки по r - 2 (nk)
Число разбиений загрузки по z - 2 (nl) Нумерация колец:
1 виток - кольца 1, 3 (слева направо)
2 виток - кольца 2, 4 (аналогично)
загрузка - 5, 7, 6, 8 (слева направо и снизу вверх) Матрица системы и вектор-столбец правой части: R1 0 0 0 0 0 0 0 -wL1 wM12 wM13 wM14 wM15 wM16 wM17 wM18 -1 0 0 0 0 0 0
0 R2 0 0 0 0 0 0 wM21 -wL2 wM23 wM24 wM25 wM26 wM27 wM28 0 -1 0 0 0 0 0
...-1 0 0 0 0 0 0
...0 -1 0 0 0 0 0
...0 0 0 0 0 0 0
...0 0 0 0 0 0 0
...0 0 0 0 0 0 0
0 0 0 0 0 0 0 R8 wM81 wM82 wM83 wM84 wM85 wM86 wM87 -wL8 0 0 0 0 0 0 0
wL1 -wM12 -wM13 -wM14 -wM15 -wM16 -wM17 -wM18 R1 0 0 0 0 0 0 0 0 0 -1 0 0 0 0
-wM21 wL2 -wM23 -wM24 -wM25 -wM26 -wM27 -wM28 0 R2 0 0 0 0 0 0 0 0 0 -1 0 0 0
...0 0 -1 0 0 0 0
...0 0 0 -1 0 0 0
...0 0 0 0 0 0 0
...0 0 0 0 0 0 0
...0 0 0 0 0 0 0
-wM81 -wM82 -wM83 -wM84 -wM85 -wM86 -wM87 wL8 0 0 0 0 0 0 0 R8 0 0 0 0 0 0 0
1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0
0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0
0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 -1 0
0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 -1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 U1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 - мнимая часть U1 Зеленым цветом отмечен вектор-столбец правой части. Структура решения: Действительные части токов колец индуктора - 2*2
Действительные части токов колец загрузки - 2*2
Мнимые части токов колец индуктора - 2*2
Мнимые части токов колец загрузки - 2*2
Действительные части витковых напряжений - 2
Мнимые части витковых напряжений - 2
Действительная часть тока индуктора - 1
Мнимая часть тока индуктора - 1 Таким образом, общее число уравнений N_eq=(ni*nj+nk*nl+w+1)*2. Синим цветом выделена система без дополнительных уравнений. Дополнительные уравнения ((w+1)*2) - уравнения для витков индуктора: сумма токов колец каждого витка равна току индуктора и сумма напряжений на витках равна напряжению на индукторе U1.
Учиться надо так, чтобы это было тебе в радость.
Сообщение отредактировал FedinMA - Воскресенье, 12.10.2008, 17:56 |
| |
| |
| FedinMA | Дата: Среда, 15.10.2008, 22:23 | Сообщение # 4 |
 Асс. каф. ФЭМАЭК
Группа: Модераторы
Сообщений: 227
Статус: Offline
| Если быть точным, то исходная матрица имеет несколько иной вид: R1 0 0 0 0 0 0 0 -wL1 wM12 wM13 wM14 wM15 wM16 wM17 wM18 -1 0 0 0 0 0 0
0 R2 0 0 0 0 0 0 wM21 -wL2 wM23 wM24 wM25 wM26 wM27 wM28 0 -1 0 0 0 0 0
...-1 0 0 0 0 0 0
0 0 0 R4 ...0 -1 0 0 0 0 0 wL1 -wM12 -wM13 -wM14 -wM15 -wM16 -wM17 -wM18 R1 0 0 0 0 0 0 0 0 0 -1 0 0 0 0
-wM21 wL2 -wM23 -wM24 -wM25 -wM26 -wM27 -wM28 0 R2 0 0 0 0 0 0 0 0 0 -1 0 0 0
...0 0 -1 0 0 0 0
-wM41 -wM42 -wM43 wL4 ...0 0 0 -1 0 0 0 0 0 0 0 R5 ...0 0 0 0 0 0 0
...0 0 0 0 0 0 0
...0 0 0 0 0 0 0
0 0 0 0 0 0 0 R8 wM81 wM82 wM83 wM84 wM85 wM86 wM87 -wL8 0 0 0 0 0 0 0 -wM51 -wM52 -wM53 -wM54 wL5 ...0 0 0 0 0 0 0
...0 0 0 0 0 0 0
...0 0 0 0 0 0 0
-wM81 -wM82 -wM83 -wM84 -wM85 -wM86 -wM87 wL8 0 0 0 0 0 0 0 R8 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0
0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0
0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 -1 0
0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 -1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 U1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 Т.е. группы строчек меняются местами, поскольку вначале формируются строчки, определяемые действительными и мнимыми уравнениями для колец индуктора, а затем аналогично для загрузки. Последние строчки остались на своих местах. В любом случае на решение системы это не влияет. Выкладываю 4 системы уравнений с решением методом, реализованным мной в Overheat до использования Model. slae.rar Система 1 состоит из 62 уравнений, системы 2, 3 и 4 - из 242 уравнений. Цель эксперимента - сравнить решения 4-х систем, полученные тремя способами:
1. Метод Гаусса, реализованный в старой версии Overheat.
2. Метод, разработанный DEADalusом.
3. Решение в среде MATLAB. Кто хочет помочь с решением, присоединяйтесь! В частности, интересным фактом является то, что системы 3 и 4 получены при исходных данных незначительно отличающихся друг от друга, однако решения отличаются катастрофически, что говорит о плохой обусловленности системы уравнений. Интересно, какие результаты дадут другие методы решения СЛАУ.
Учиться надо так, чтобы это было тебе в радость.
|
| |
| |
| FedinMA | Дата: Понедельник, 20.10.2008, 20:52 | Сообщение # 5 |
 Асс. каф. ФЭМАЭК
Группа: Модераторы
Сообщений: 227
Статус: Offline
| Получил некоторые результаты.
Решения 4-х СЛАУ в среде MATLAB в целом близки к решениям, полученным в старой версии Overheat. Визуально (путем сравнения нескольких первых и последних чисел вектор-столбца решения) решения для системы №1 почти не отличаются, для 2 - аналогично, 3,4 - есть отличия. Желательно, используя приведенную выше структуру решения, провести более детальное сравнение и построить графики.
Вот полученные результаты:
slae-2.rar
А вот числа обусловленности матрицы A:
№1 - 1.639479047322362e+004
№2 - 9.007142765818338e+003
№3 - 5.622203322062834e+003
№4 - 5.622221540341978e+003,
которые рассчитаны в MATLAB 7.0.4 с использованием функции cond(A), возвращающей число обусловленности матрицы, основанное на второй норме, т.е. отношение самого большого сингулярного числа А к самому малому.
Подчеркну, что значение cond(A), близкое к 1, указывает на хорошо обусловленную матрицу.
Таким образом, все четыре матрицы являются очень плохо обусловленными, что означает высокую чувствительность решений соответствующих СЛАУ к погрешностям (или небольшим изменениям) исходных данных. Исследуемые матрицы являются также и достаточно сильно разреженными. Ниже для примера представлена графическое отображение матрицы №4 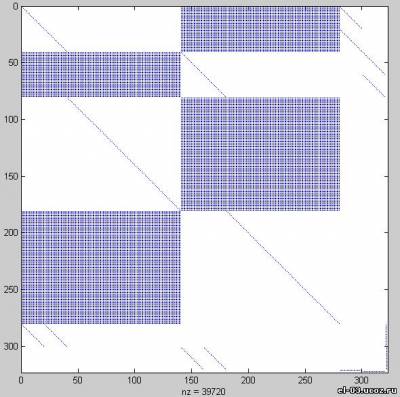
Данное графическое представление будет характерно и для остальных 3-х матриц. Нашел в результате этих вычислений опечатку
Quote (FedinMA) Таким образом, общее число уравнений N_eq=(ni*nj+nk*nl+w+1)*2.
Следует читать
Таким образом, общее число уравнений N_eq=(ni*nj*w+nk*nl+w+1)*2.
Учиться надо так, чтобы это было тебе в радость.
|
| |
| |
| FedinMA | Дата: Пятница, 21.11.2008, 17:18 | Сообщение # 6 |
 Асс. каф. ФЭМАЭК
Группа: Модераторы
Сообщений: 227
Статус: Offline
| Сравнение результатов Overheat и MATLAB провел: отличия, к сожалению, незначительные и не оказывают почти никакого влияния на полученные зависимости... На самом деле особенных отличий и не должно было быть, поскольку MATLAB, как выяснилось, не осуществляет никакого предобуславливания СЛАУ. Для решения таких СЛАУ нужно использовать либо специализированные расчетные пакеты (в свободном доступе пока таких не нашел), либо самим осуществлять регуляризацию.
Далее привожу некоторые свои соображения по поводу вопросов плохой обусловленности и способов борьбы с ней при решении СЛАУ (то, что пока понял сам).
Итак, рассмотрим все на примере матрицы 2х2 (см. рис. 1)
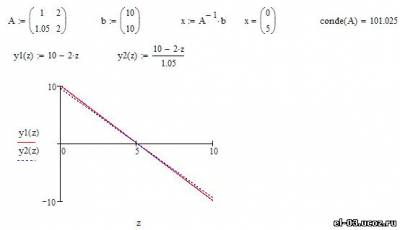
На рисунке приведена геометрическая интерпритация понятия плохой обусловленности матрицы. Действительно, решение данной СЛАУ определяется точкой пересечения прямых, и небольшое изменение в наклоне этих прямых приведет к катастрофическому изменению решения, поскольку прямые эти почти параллельны. Для хорошо обусловленных систем две прямые пересекаются под значительным углом и небольшие изменения в их наклоне не оказывают существенного влияния на точку пересечения.
Теперь рассмотрим другую систему, незначительно отличающуюся от предыдущей (см. рис. 2)

Без использования метода регуляризации получено решение, существенно отличающееся от решения предыдущей СЛАУ. И это при числе обусловленности около 100 (у нас 5000 - 10000 и более).
С использованием регуляризации получаем решение, которое является практически таким же, как и решение исходной СЛАУ.
Суть метода регуляризации состоит в том, что к исходной СЛАУ присовокупляется априорная информация, которая может быть как количественной, так и качественной.
С использованием количественной информации - см. рис. 1,2.
Как использовать качественную информацию пока не разобрался.
Таким образом имеются следующие направления в этом направлении:
1. Дальнейшее изучение решения некорректных задач (методы регуляризации Тихонова А.Н.).
2. Возможно ли использование количественной информации? Возможно, необходимо использовать пробные решения или что-то вроде того. Кстати, скорее всего так и работает Model. Это я вскоре проверю и напишу что получилось.
3. Как использовать качественную информацию о решении???
Учиться надо так, чтобы это было тебе в радость.
|
| |
| |
| DVK | Дата: Четверг, 27.11.2008, 18:47 | Сообщение # 7 |
|
Группа: Удаленные
| Не пойму, чем второе решение не нравится. Оно ведь более верное, чем третье.
 Добавлено (27.11.2008, 18:47)
---------------------------------------------
Что-то мне подсказывает, что проблема в самой СЛАУ, тоесть в способе её формирования. Повидимому, этот способ не является адекватным тем физическим процессам, которые "как-бы" описываюся этой самой СЛАУ.
А "присовокупление априорной информации" это какие-то пляски с бубном 
Решение #2 ближе к истине, чем решение #3. Поэтому именно его можно считать математически верным.
Сообщение отредактировал DVK - Четверг, 27.11.2008, 18:53 |
| |
| |
| FedinMA | Дата: Четверг, 27.11.2008, 22:09 | Сообщение # 8 |
 Асс. каф. ФЭМАЭК
Группа: Модераторы
Сообщений: 227
Статус: Offline
| Quote (DVK) Не пойму, чем второе решение не нравится. Оно ведь более верное, чем третье.
Quote (DVK) Решение #2 ближе к истине, чем решение #3. Поэтому именно его можно считать математически верным.
В том и дело, что решение 1 и 2 - это решения систем, которые почти не отличаются. Представь такую ситуацию: при формировании системы элементы матрицы получились немного другими (пусть порядок абсолютной погрешности 10^-3, как в примере, или, скажем, 10^-10) за счет, скажем, округления при их расчете на этапе формирования матрицы. В одном случае мы получим решение 1, в другом - решение 2, которые отличаются катастрофически. Т.е. суть метода регуляризации получить решение, с одной стороны, максимально приближенное к точному решению данной системы (это решение 2), а с другой - максимально приближенное к решению 1. Обоим этим критериям удовлетворяет только решение 3. Данная задача решается выбором оптимального значения параметра регуляризации, что является отдельной проблемой. Quote (DVK) Что-то мне подсказывает, что проблема в самой СЛАУ, тоесть в способе её формирования. Повидимому, этот способ не является адекватным тем физическим процессам, которые "как-бы" описываюся этой самой СЛАУ.
СЛАУ формируется в соответствии с методом индуктивно связанных контуров - получается система уравнений по второму закону Кирхгофа + несколько уравнений по первому закону Кирхгофа. Метод применим для линейных систем, т.е. и в случае нагрева неферромагнитной загрузки в цилиндрическом индукторе.
Учиться надо так, чтобы это было тебе в радость.
|
| |
| |
| DVK | Дата: Четверг, 27.11.2008, 22:54 | Сообщение # 9 |
|
Группа: Удаленные
| Quote (FedinMA) Представь такую ситуацию: при формировании системы элементы матрицы получились немного другими (пусть порядок абсолютной погрешности 10^-3, как в примере, или, скажем, 10^-10) за счет, скажем, округления при их расчете на этапе формирования матрицы.
Может разрядность повысить? Скажем, до 64 бит на число? Quote (FedinMA) суть метода регуляризации получить решение, с одной стороны, максимально приближенное к точному решению данной системы (это решение 2), а с другой - максимально приближенное к решению 1.
Но для этого нужно знать решение #1, верно?
|
| |
| |
| FedinMA | Дата: Пятница, 28.11.2008, 00:02 | Сообщение # 10 |
 Асс. каф. ФЭМАЭК
Группа: Модераторы
Сообщений: 227
Статус: Offline
| Quote (DVK) Может разрядность повысить? Скажем, до 64 бит на число? Возможно это поможет. Есть еще вариант - проводить все операции над числами в дробном виде и, тем самым, исключить все округления.
Учиться надо так, чтобы это было тебе в радость.
|
| |
| |
| |






