 | |  |
| |
Анализ гармонического состава кривой фазного тока для оценки распределения мощности в тигле рудно-термической печи
Анализ гармонического состава кривой фазного тока для оценки распределения мощности в тигле рудно-термической печи
В.П. Рубцов, В.А. Елизаров
Рудно-термические печи (РТП) получили широкое распространение во многих отраслях современной промышленности. Так, например, в черной и цветной металлургии их применяют для выплавки ферросплавов и чугуна, в огнеупорном производстве – для получения плавленых огнеупоров, а в химической отрасли – для выплавки карбида кальция, фосфора и т.д. Подавляющая часть процессов в РТП заключается в восстановлении природных руд или концентратов специальными восстановителями (углерод, кремний, алюминий) при высоких температурах, развиваемых в ванне печи [1]. Большая часть РТП работает на переменном токе, и эти печи являются крупными потребителями электроэнергии. Печи, как правило, питают через один понизительный трехфазный печной трансформатор (или три однофазных) от сети переменного тока промышленной частоты от самостоятельных подстанций с напряжением на высокой стороне 110 или 220 кВ. Короткие сети печей способны пропускать токи близкие к 150 кА. Установленные мощности единичных агрегатов достигают 250 МВА и более. Расход электроэнергии значителен и, в зависимости от вида получаемого продукта, достигает 3-10 (МВт ч)⁄т [2, 3]. Рудно-термические печи работают в непрерывном режиме, который может длиться несколько месяцев. Капитальный ремонт с полной заменой футеровки происходит один раз в 1,5-2 года. Все указанные особенности РТП предъявляют высокие требования к надежности конструкций печей и ее электрооборудования. Обеспечение эффективной работы РТП является важной проблемой, которую решают путем совершенствования как их конструкций и электрооборудования, так и систем автоматического управления. Большое влияние на эффективность работы РТП оказывает распределение мощности, выделяемой в шихте, электрической дуге и расплаве. Знание распределения мощности в ванне печи и управление им можно рассматривать как эффективный способ достижения рационального экономичного режима работы печи. Для определения распределения мощности в ванне РТП необходимо знать распределение токов в ней, однако этому вопросу на данный момент уделено мало внимания. Первые исследования распределения электрического тока в ферросплавных печах были выпол¬нены в Днепропетровском металлургическом институте под руководством профессора С. И. Тельного в 1938 г. В дальнейшем такие исследования проводили А. С. Микулинский, Г. А. Сисоян, Д. А. Диамидовский, Г. Ф. Платонов и др. На действующих ферросплавных печах подобные исследования проводил И. Т. Жердев [4, 5]. Вместе с тем задача определения распределения тока в ваннах РТП до сих пор не нашла решения. Предложенные рядом авторов аналитические методы расчета распределения тока очень сложны и не позволяют получить точные результаты. Кроме того, при использовании аналитических методов требуется знание параметров шихты и расплава, точность определения которых крайне низка. Методы исследования распределения тока в ваннах РТП, применяемые в настоящее время, требуют выполнения длительных измерений напряжений и токов, дают недостаточно точные результаты и, кроме того, не применимы для ванны с неодно¬родной средой [6], т.е. для ванн, в которых вещества находятся в разных агрегатных состояниях. В настоящей статье рассматривается возможность оценки теплового режима в ваннах РТП с закрытой дугой по гармоническому составу кривой фазного тока. Характерной особенностью работы РТП с закрытой дугой, затрудняющей выбор режима работы печи и процесса управления режимом плавки, является горение дуги под слоем шихты в газовом пузыре – тигле, стенки которого образуются постепенно сходящей вниз и плавящейся шихтой. Внутри тигля происходят восстановительные реакции. В каждый момент времени дуга оказывается шунтированной проводящими стенками тигля. В результате мощность, расходуемая на плавление шихты, проведение восстановительных реакций и поддержание расплава в жидком состоянии, выделяется как в электрической дуге, горящей между электродом и расплавом, так и в стенках тигля, представляющих собой активное сопротивление. Схема на рис. 1 иллюстрирует наиболее вероятные пути растекания токов в ванне РТП с закрытой дугой. Трехфазное напряжение (на схеме A, B, C) от вторичной обмотки трансформатора (на схеме условно не показан) подают на электроды, число которых, в большинстве случаев, соответствует числу фаз трансформатора. Замыкание фазных токов I_A,I_B,I_С происходит через расплав, собирающийся в нижней части печи, поскольку для питания РТП, как правило, используют схему с изолированной нейтралью. Пути растекания токов в ванне печи обозначены штриховыми линиями. Для каждой фазы печи можно выделить следующие составляющие токов: I – общий фазный ток печи; I_д – ток в дуговом промежутке; I_ш – ток, протекающий по проводящим стенкам тигля; I_мэ – ток, протекающий от электрода к электроду по шихте. Следует отметить, что измерению поддаются только фазные токи печи I. Значения токов I_д и I_ш могут быть определены только расчетным путем. Рис. 1. Разрез ванны рудно-термической печи с закрытой дугой (обозначения в тексте) Рис. 1. Разрез ванны рудно-термической печи с закрытой дугой (обозначения в тексте)
Эффективная работа РТП, обеспечивающая равномерный нагрев реакционной зоны печи без перегревов и подстываний, становится возможной при определенном соотношении мощностей, выделяемых в дуговом промежутке и в проводящих стенках тигля. В настоящее время объективных методов контроля распределения мощностей в ванне РТП не существует, что обусловлено недоступностью измерения соответствующих токов, протекающих в ванне печи. Выбор режима работы печи, как правило, определяется интуицией оператора или опытом эксплуатации аналогичных установок. Электрический расчет токов в РТП с закрытой дугой удобно проводить по схеме замещения, представленной на рис. 2, составленной на основе электрической схемы [1]. Шунтирующие сопротивления футеровки не учитываются. Элементы электрической цепи представлены активными и индуктивными сопротивлениями, подобранными таким образом, чтобы при одинаковых внешних напряжениях токи и мощности действительной схемы и схемы замещения были равны. Сопротивление дуги принято чисто активным и представлено семейством вольтамперных характеристик, функций тока и длины дуги, т.е. R_д=u_д(i_д,l_д ). Сопротивление подводящих кабелей первичного контура не учитываются в виду их малости. Трансформатор представляется совокупностью активного и индуктивного сопротивлений.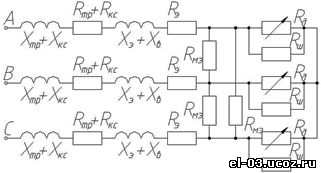 Рис. 2. Трехфазная схема замещения рудно-термической печи: R_кс и X_кс – активное и индуктивное сопротивления короткой сети и токоподвода; R_тр и X_тр – активное и индуктивное сопротивление трансформатора; R_э и X_э – активное и индуктивное сопротивление электрода; X_в – индуктивное сопротивления ванны; R_д – активное сопротивление дугового промежутка; R_ме – активное сопротивление материалов в ванне печи между электродами; R_ш – активное сопротивление шихты на пути тока от боковой поверхности электрода к металлу (сопротивление тигля) Рис. 2. Трехфазная схема замещения рудно-термической печи: R_кс и X_кс – активное и индуктивное сопротивления короткой сети и токоподвода; R_тр и X_тр – активное и индуктивное сопротивление трансформатора; R_э и X_э – активное и индуктивное сопротивление электрода; X_в – индуктивное сопротивления ванны; R_д – активное сопротивление дугового промежутка; R_ме – активное сопротивление материалов в ванне печи между электродами; R_ш – активное сопротивление шихты на пути тока от боковой поверхности электрода к металлу (сопротивление тигля) Рис. 3. Однофазная схема замещения фазы рудно-термической печи: X – индуктивное сопротивление короткой сети, включающее в себя индуктивное сопротивление обмотки трансформатора и токоподвода; R – активное сопротивление короткой сети, состоящее из активного сопротивления трансформатора, токоподвода и электрода; R_ш – сопротивление материала шихты (тигля), шунтирующего дугу; R_д – нелинейное сопротивление дуги, зависящее от тока Рис. 3. Однофазная схема замещения фазы рудно-термической печи: X – индуктивное сопротивление короткой сети, включающее в себя индуктивное сопротивление обмотки трансформатора и токоподвода; R – активное сопротивление короткой сети, состоящее из активного сопротивления трансформатора, токоподвода и электрода; R_ш – сопротивление материала шихты (тигля), шунтирующего дугу; R_д – нелинейное сопротивление дуги, зависящее от тока
 Система уравнений (1) была упрощена и переведена при помощи преобразований Лапласа в операторную форму: Нелинейное сопротивление дуги R_д(I_д ) в выражении (2) удобно представить в виде вольт-амперной характеристики (ВАХ). Однако, как известно, по мере удлинения дуги переменного тока происходит изменение формы ее ВАХ [7]. С целью упростить моделирование и сократить число варьируемых параметров ВАХ дуги аппроксимирована знаковой функции u_д=U_д∙sign(i_д) [8], т.е. принято условие независимости напряжения дуги от тока. Такое допущение не вносит больших погрешностей в результаты исследований, так как реальная ВАХ закрытой дуги в РТП на рабочем участке незначительно зависит от тока. Влияние формы кривой ВАХ на гармонический состав токов целесообразно проводить на более поздней стадии исследования после того, как будут выявлены основные факторы, влияющие на гармонический состав токов и распределение мощностей, и установлена возможность идентификации режима работы РТП по гармоническому составу кривой фазного тока. Для учета динамических свойств дуги в схему модели дополнительно введено инерционное звено первого порядка с постоянной времени дуги T_д. Значение постоянной времени дуги, шунтированной шихтой, получено при анализе экспериментальных данных [9] и составляет 1,1∙10^-4 с. Отношение индуктивности короткой сети к величине активного сопротивления – постоянная времени короткой сети T_к=L/R. Систему уравнений (2) удобно представить в виде структурной схемы, приведенной на рис. 4, которая является более наглядной формой записи системы уравнений (2), и позволяет упростить её исследование. Рис. 4. Структурная схема фазы рудно-термической печи Рис. 4. Структурная схема фазы рудно-термической печи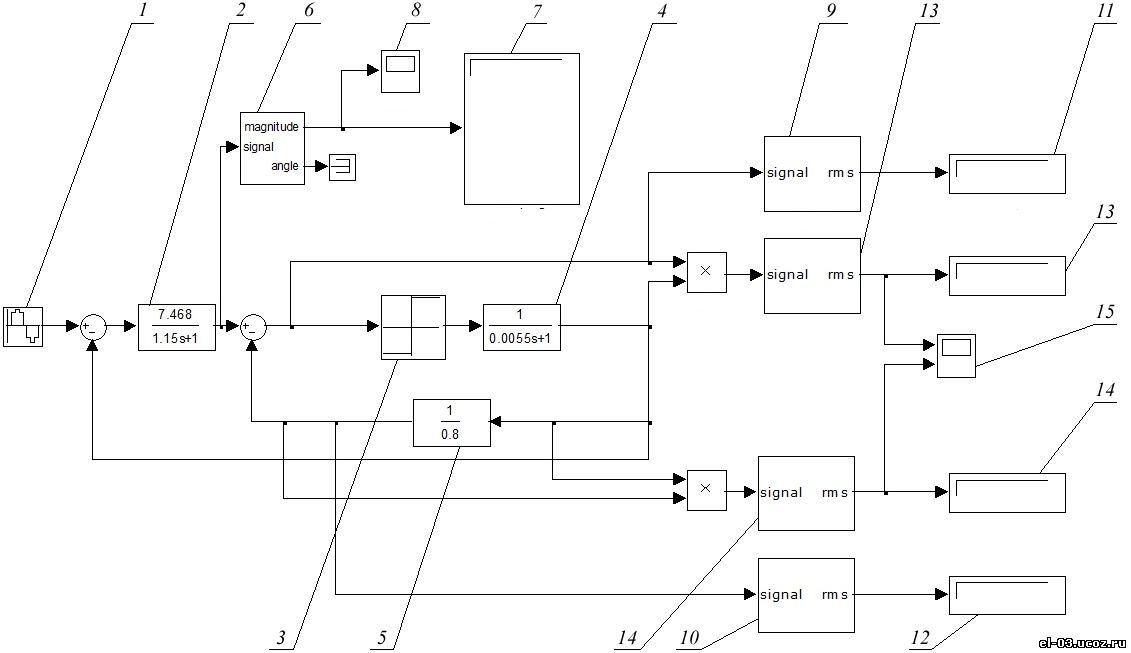 Рис. 5. Схема модели для одной фазы печи в пакете программ MatLab Simulink (обозначения в тексте) Рис. 5. Схема модели для одной фазы печи в пакете программ MatLab Simulink (обозначения в тексте)
Основным недостатком численных методов решения является невозможность получения общих решений. Для получения обобщенных зависимостей, инвариантных к типу печи, была разработана система относительных величин. В качестве базовых величин приняты номинальные параметры ферросплавной печи для получения ферросилиция, так как агрегаты данного типа в настоящее время наиболее распространены в промышленности (около 60% всего ферросплавного производства) [10]. Анализ электрических параметров печей (ток, напряжение, активное и индуктивное сопротивление короткой сети) [11] показал, что они изменяются в ограниченных пределах, что позволяет распространить результаты на весь класс печей. В качестве объекта исследования была принята ферросплавная печь РКО-16,5, параметры которой приведены в табл. 1. Сопротивление ванны печи, включающее в себя сопротивление твердой шихты стенок тигля и плазмы электрической дуги, принято, согласно работе [12], равным R_в=1,038 мОм.
Таблица 1. Основные параметры базовой печи РКО-16,5
Параметр
| Значение параметра
| Установленная мощность трансформатора, МВА
| 16,5
| Рабочий ток в электроде, кА
| 63
| Рабочее напряжение, В
| 175
| Частота питающей сети, Гц
| 50
| Реактивное сопротивление, мОм:
трансформатор
короткая сеть
электроды и ванна
печная установка на фазу
| 0,121
0,453
0,416
0,990
| Активное сопротивление, мОм:
трансформатор
короткая сеть
переходные сопротивления, контактная плита-электрод
электрод
печная установка на фазу
| 0,027
0,043
0,027
0,042
0,139
|
За базовые приняты также следующие величины: базовое время, равное периоду сетевого напряжения t_б=1/f=0,02 с, базовое напряжение, равное рабочему напряжению U_б=U_раб=175,0 В, базовый ток, равный рабочему току в электроде I_б=I_раб=63000 А.
Относительные величины определены и обозначены следующим образом: время: τ*=t/t_б; постоянная времени короткой сети и трансформатора: T_к*=T_к/t_б; постоянная времени дуги: T_д*=T_д/t_б; круговая частота: ω*=2∙π∙f∙t_б; напряжение: u*=u/U_б ; ток: i*=i/I_б ; активное сопротивление короткой сети: r_к*=R/R_б ; сопротивление дуги: r_д*=R_д/R_б ; сопротивление шихты: r_ш*=R_ш/R_б; суммарная мощность: p*=P/(I_б∙U_б); мощность дуги: p_д*=P_д/(I_б∙U_б); мощность шихты p_ш^*=P_ш/(I_б∙U_б).
Адекватность разработанной модели проверена путем сравнения амплитудных значений гармонических составляющих (1, 3, 5 и 7 гармоник) фазного тока, полученных на модели в дуговом режиме с экспериментальными данными, снятыми на действующих дуговых сталеплавильных печах переменного тока ДСП-100Н3А [9], ДСП-25 и ДСП-10 [13].
Гармонические составляющие тока и напряжения в работе [9] были выделены с использованием полосовых фильтров, настроенных на частоты 50, 150, 250 и 350 Гц. Современная измерительная техника в сочетании с компьютерными технологиями позволяет получить экспериментальные данные о гармоническом составе кривой фазного тока и напряжения на основе осциллограмм, снятых на действующей печи.
Приемлемое совпадение результатов расчета на модели с литературными данными [9, 12] свидетельствует об адекватности разработанной модели (табл. 2). Наличие расхождений в значениях (до 14%) может быть обусловлено погрешностями эксперимента, а также принятыми в процессе моделирования допущениями.
Таблица 2. Сравнение результатов расчета на модели с литературными данными для печи ДСП-25.
Номер
гармонической
составляющей
| Доля гармонических составляющих, %
| Погрешность, %
| Результаты
вычисления
| Результаты
эксперимента
| 1
| 100
| 100
| 0
| 3
| 5,253
| 5,2 | 1,02 | 5
| 1,893
| 2,2 | 13,95 | 7
| 0,9659
| 1,0 | 3,41 |
В процессе исследования на модели проанализировано влияние напряжения на дуге u_д* и сопротивления шихты r_ш* на гармонический состав кривой фазного тока (определены амплитудные значения первой i_m1*, третьей i_m3*, пятой i_m5* и седьмой i_m7* гармонических составляющих фазного тока i*), а также на действующие значения суммарной мощности, выделяемой в ванне РТП p*=p_ш*+p_д*, мощности в дуге p_д* и мощности, выделяемой в шихте p_ш*. Так как кривая фазного тока симметрична, значения четных гармонических составляющих равны нулю. Напряжение дуги u_д* в процессе исследования изменяли в пределах 0,1≤u_д*≤0,9, сопротивление шихты – в пределах 0,2≤r_ш*≤0,9.
Так как при работе РТП автоматический регулятор мощности, как правило, поддерживает постоянным фазный ток [14], для получения зависимостей, отражающих реальный режим работы печи, исследования на модели проведены при неизменном значении фазного тока, т.е. при i*≈const.
В процессе исследования рассчитаны и выведены на осциллографы 8, 17 и дисплеи 7, 11, 12, 15, 16 (рис. 5) переходные функции i_m1*(τ), i_m3*(τ), i_m5*(τ), i_m7*(τ) и мощностей p*(τ),p_ш*(τ),p_д*(τ). Установившиеся значения указанных величин записаны с помощью виртуальных дисплеев. По полученным данным были построены зависимости в функции отношения токов (i_^*)/i* амплитудных значений гармонических составляющих токов i_m1* (i_ш*/i*), i_m3*(i_ш*/i*), i_m5*(i_ш*/i*), i_m7*(i_ш*/i*), а также зависимости действующих значений мощностей p* (i_ш*/i*), p_ш*(i_ш*)/i*), p_д*(i_ш*/i*).
В качестве примера на рис. 6 и рис. 7 приведены рассчитанные на модели зависимости амплитуды гармонических составляющих i_m3*,i_m5*,i_m7* и мощностей p*,p_д*,p_ш* от отношения токов i_ш*/i* при относительном сопротивлении шихты r_ш*=0,5 и изменении напряжения дуги u_д* от 0,1 до 0,9. Указанные зависимости показывают, что наблюдается связь между гармоническим составом кривой фазного тока и распределением токов и мощностей в дуге и в шихте.
 Рис. 6. Зависимости относительных значений амплитуд третьей, пятой и седьмой гармонической составляющей фазного тока от отношения тока, протекающего в шихте к полному току печи Рис. 6. Зависимости относительных значений амплитуд третьей, пятой и седьмой гармонической составляющей фазного тока от отношения тока, протекающего в шихте к полному току печи Рис. 7. Зависимости относительных значений полной мощности, мощности, выделяемой в дуге, и мощности, выделяемой в шихте, от отношения тока, протекающего в шихте к полному току печи Рис. 7. Зависимости относительных значений полной мощности, мощности, выделяемой в дуге, и мощности, выделяемой в шихте, от отношения тока, протекающего в шихте к полному току печи
В то же время соотношение токов, протекающих по шихте и дуге, оказывает значительное влияние на изменение высших гармонических составляющих тока, в частности третьей гармонической составляющей. Как следует из сопоставления зависимостей, приведенных на рис. 6, амплитуда третьей гармоники тока i_m3* изменяется от значения i_m3*=0,01 до i_m3*=0,022, т.е. практически в 2 раза, при изменении отношения тока шихты к полному току в диапазоне 0,2≤i_ш*/i*≤0,5. В этом случае сопротивление шихты превосходит сопротивления дуги и, следовательно, через дугу протекает больший ток. При этом, как показывает рис. 7, соответствующим образом распределяются мощности дуги p_д* и шихты p_ш*.
Проведенный анализ показывает, что между гармоническим составом фазного тока РТП с закрытой дугой и распределением мощностей в ванне печи имеется явно выраженная зависимость, которая может быть использована для идентификации теплового режима в печи. Для этого по полученным в ходе эксперимента данным были построены зависимости мощности, выделяемой в дуге, от амплитуды третьей гармонической составляющей фазного тока. В качестве примера на рис. 8 приведена рассчитанная на модели зависимость мощности дуги от амплитуды третьей гармонической составляющей при относительном сопротивлении шихты r_ш*=0,5 и изменении напряжения дуги u_д* от 0,1 до 0,9 (в относительных единицах).
 Рис. 8. Связь относительного значения мощности дуги и амплитуды третьей гармонической составляющей фазного тока Рис. 8. Связь относительного значения мощности дуги и амплитуды третьей гармонической составляющей фазного тока
Использование такой зависимости в системах автоматического управления в силу её неоднозначности затруднено. Поэтому кривая, приведенная на рис. 8, может быть линеаризована и получено соответствующее уравнение для вычисления мощности дуги по величине амплитуды третьей гармонической составляющей. Погрешность такого допущения не должна превышать 10 %.
Мощность, выделяемая в ванне печи, может быть рассчитана по измеренной силе тока в электроде и напряжению ванны печи как их среднеквадратичное (действующее) значение  . Применение зависимости, показанной на рис. 8 позволяет определить долю мощности, выделяемую в дуге по значению третьей гармонической составляющей фазного тока, мощность, выделяемая в шихте, вычисляется по выражению: P_ш=P-P_д. . Применение зависимости, показанной на рис. 8 позволяет определить долю мощности, выделяемую в дуге по значению третьей гармонической составляющей фазного тока, мощность, выделяемая в шихте, вычисляется по выражению: P_ш=P-P_д.
Кроме того, информативной оказалась зависимость токов, протекающих через дугу i_д* и шихту i_ш* от сопротивления шихты, приведенная на рис. 9 при постоянном напряжении на дуге u_д*. Анализируя полученные зависимости можно сделать следующие выводы. Левая часть графика рис. 9 (при изменении сопротивления шихты r_ш* от 0,1 до 0,18) характеризует работу печи с высокой проводимостью шихты, когда большая часть тока ответвляется на шихту или кокс. С увеличением сопротивления шихты ток через нее уменьшается, а ток, протекающий через торец электрода и расплав, возрастает. Это означает, что для обеспечения заданной мощности при постоянном напряжении по мере увеличения сопротивления шихты следует увеличивать посадку электродов в шихту или расплав.
 Рис. 9. Зависимость токов, протекающих через дугу и шихту от сопротивления шихты Рис. 9. Зависимость токов, протекающих через дугу и шихту от сопротивления шихты
Таким образом, полученные зависимости дают возможность охарактеризовать режим работы печи и определить распределение мощности в ванне печи. Правая часть графика рис. 9 характеризует работу печей, у которых роль шихтовой проводимости незначительна. Полученные зависимости полностью совпадают с аналогичными зависимостями для действующих печей, приведенные в работе [15], что еще раз свидетельствует о правильности и правомерности сделанных ранее допущений.
Определение желаемого соотношения мощностей, выделяемых в дуге и в шихте РТП и, следовательно, значения измеряемой высшей гармоники, которое можно поддерживать в процессе плавки, зависит в первую очередь от вида выплавляемого сплава. Окончательный выбор оптимальных мощностей, выделяемых в дуге и в шихте возможен только на основе теплового расчета.
Проведенный анализ гармонического состава кривой фазного тока может быть использован для получения экспериментальных данных о распределение мощностей в ванне печи.
Полученные в ходе исследования результаты планируется применять для модернизации существующих систем автоматического регулирования режимом РТП, а также во вновь разрабатываемых печах и системах управления.
Список литературы
- Электрические и промышленные печи. Дуговые печи и установки специального нагрева. / Под ред. А. Д. Свенчанского. М.: Энергоиздат, 1981. 296 с.
- Промышленные установки электродугового нагрева и их параметры. / Под ред. Л. Е. Никольского. М.: Энергия, 1971. 272 с.
- Миронов Ю.М., Миронова А.Н. Электрооборудование и электроснабжение электротермических, плазменных и лучевых установок. М.: Энергоатомиздат, 1991. 376 с.
- Жердев И.Т., Даватц В.Н., Поляков И.И. Исследование строения рабочего пространства ферросилициевой печи. // Черная металлургия. 1960. №9. С. 20-25.
- Жердев И.Т., Яськов Е.С., Корневич А.Л. Распределение мощности в ванне силикомарганцевой печи. // Электротермия. 1974. №3. С. 12-13.
- Марков Н.А., Чердовских П.П. Распределение электрического тока в ванне дуговой печи. М.: Энергия, 1966. 104 с.
- Сисоян Г.А. Электрическая дуга в электрической печи. М.: Металлургия, 1971. 304 с.
- Хаинсон А.В. О точности расчета электрической цепи ДСП. Математическое моделирование и расчет дуговых и плазменных сталеплавильных печей. Сборник научный трудов ВНИИЭТО. М.: Энергоатомиздат, 1982. С. 53-56.
- Гордиенко В.А., Дрогин В.И., Попов А.Н., Пирогов Н.А. Расчет и измерение напряжения дуги ДСП. Математическое моделирование и расчет дуговых и плазменных сталеплавильных печей. Сборник научных трудов ВНИИЭТО. М.: Энергоатомиздат, 1982. С. 49-53.
- Рысс М.А. Производство ферросплавов. М.: Металлургия, 1985. 344 с.
- Короткие сети и электрические параметры дуговых печей. / Под ред. Я.Б.Данциса и Г.М. Жилова. М.: Металлургия, 1987. 320 с.
- Жданов А.В., Заякин О.В., Жучков В.И. Изучение электросопротивления материалов и шихт, применяемых для получения ферромарганца. // Электрометаллургия. 2007. №6. С.24-27.
- Минеев Р. В., Михеев А.П. Электродинамика дуговых сталеплавильных печей в задачах оптимизации электроснабжения. Современное состояние электропечестроения (по материалам VII международного конгресса по электротермии). Дуговой нагрев и новые виды нагрева. М.: ВНИИЭМ, 1975. С.23-39.
- Электрооборудование и автоматика электротермических установок. / под ред. А.П. Альтгаузена, М.Д. Бершицкого, М.Я. Смелянского и В.М. Эдемского. М.: Энергия, 1978. 304 с.
- Платонов Г.Ф. Параметры и электрические режимы металлургических электродных печей. М.: Энергия, 1965. 151 с.
Электрометаллургия. - 2011. - №3. - С. 11-19.
|
| Категория: Статьи | Добавил: DEADalus (05.04.2011)
|
| Просмотров: 4114 | Комментарии: 1
| Рейтинг: 0.0/0 |
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] | |
 | |  |
|
| Статистика |

Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
|






