 | |  |
| |
Анализ гармонического состава формы кривой фазного тока для оценки теплового режима в рудно-термической печи с закрытой дугой
Анализ гармонического состава формы кривой фазного тока для оценки теплового режима в рудно-термической печи с закрытой дугой
В.П. Рубцов, В.А. Елизаров
Введение
Руднотермические (РТП) и рудовосстановительные (РВП) печи широко применяются для получения чистых металлов или сплавов путем восстановления их окислов из руд (ферросилиций, ферромарганец, силикомарганец, феррохром) или концентратов (ферровольфрам, ферромолибден, феррованадий, ферротитан) [1]. РТП используют для получения фосфора, карбида кальция, а также для расплавления базальта, диабаза и т.п. минералов. Печи этого типа, как правило, работают на переменном токе и являются крупными потребителями электроэнергии. Установленная мощность трансформаторов для питания РТП достигает 250 МВА и более. Их питание осуществляется от трехфазной сети, как правило, от самостоятельных подстанций с первичным напряжением 110 или 220 кВ. Обычно РТП имеют три электрода, расположенных по треугольнику (круглые печи) или вытянутых в линию (прямоугольные печи). Печи работают непрерывно, капитальный ремонт с заменой футеровки осуществляют один раз в 1,5–2 года, что предъявляет высокие требования к надежности конструкции печи и к ее электрооборудованию. Обеспечение энергетической эффективности работы РТП является важной задачей, которая решается путем совершенствования, как их конструкций и электрооборудования, так и систем автоматического управления процессом плавки.
Основной особенностью РТП с закрытой дугой, затрудняющей выбор режима работы печи и осложняющий процесс управления режимом плавки, является горение дуги под слоем шихты (так называемого «колошника»). Это приводит к образованию дополнительного контура протекания тока через шихту, шунтирующего дугу. В результате энергия, обеспечивающая нагрев шихты и расплава, поступает от двух источников: электрической дуги, горящей между электродом и расплавом, и токами, протекающими по шихте, которая является активным сопротивлением. Эффективность работы РТП, достигается при определенном соотношении мощностей, выделяемых в дуге и шихте, обеспечивающих равномерный нагрев без перегрева и охлаждения отдельных участков печи [2]. Однако объективные методы контроля распределения мощностей и температур в ванне РТП в настоящее время отсутствуют, что обусловлено недоступностью измерения токов, протекающих в ней. Поэтому выбор режима работы печи в значительной степени определяется интуицией плавильщика или опытом эксплуатации подобных агрегатов.
В данной статье анализируется возможность контроля распределения мощности и теплового режима РТП с закрытой дугой по гармоническому составу кривой фазного тока, искажения которого обусловлены нелинейностью вольт-амперной характеристики дуги.
Разработка модели РТП с закрытой дугой
Пути растекания токов в ванне РТП с закрытой дугой иллюстрирует схема, приведенная на рис. 1 [3]. Трехфазное напряжение (фазы А, В и С) от вторичной обмотки трансформатора (на схеме не показан) подается на три электрода Э. Для питания РТП используется схема с изолированной нейтралью, что обуславливает замыкание фазных токов IА, IВ, IС через расплав, находящийся в нижней части ванны печи. Пути растекания токов в ванне печи обозначены на рис. 1 стрелками. Согласно схеме рис. 1, можно выделить следующие составляющие токов, протекающих в ванне печи: I – общий ток фазы; IД – ток дуги; IШ – ток шихты, протекающий по тиглю, в котором горит дуга; IМЭ – ток, протекающий по шихте между электродами. Измерению поддаются только полные фазные токи I. Составляющие токов IД и IШ могут быть определены только расчетным путем.
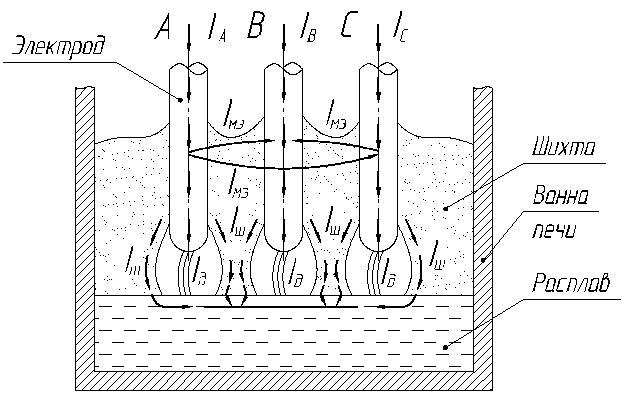 Рис. 1. Разрез руднотермической печи с закрытыми дугами. Рис. 1. Разрез руднотермической печи с закрытыми дугами.
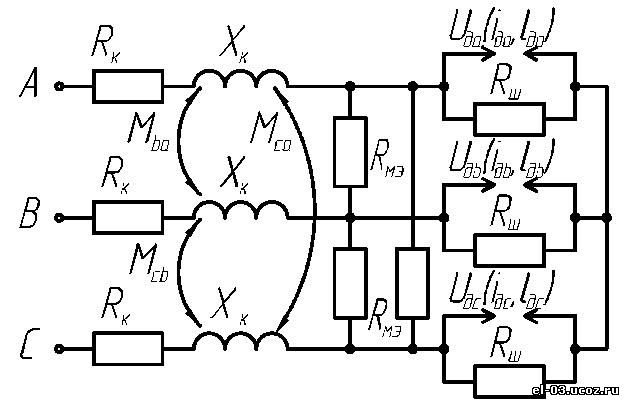 Рис. 2. Схема замещения РТП Рис. 2. Схема замещения РТП
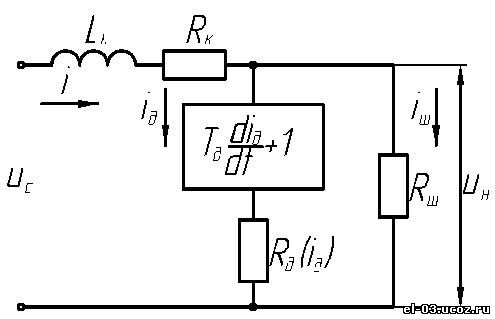 Рис. 3. Схема замещения РТП одной фазы Рис. 3. Схема замещения РТП одной фазы На основании законов Кирхгофа для схемы рис. 3 может быть записана следующая система уравнений электрического равновесия для мгновенных значений: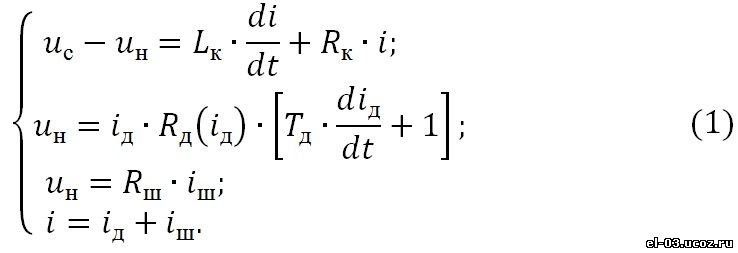 Представим уравнения системы (1) в операторной форме и упростим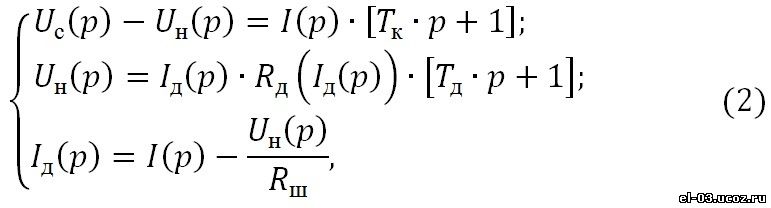 где Tк=Lк⁄Rк – постоянная времени короткой сети; Rд (I_д (p)) – нелинейное сопротивление, определяемое вольтамперной характеристикой дуги. По уравнениям системы (2) построена структурная схема, приведенная на рис. 4. С целью упрощения системы (2) и сокращения числа варьируемых параметров вольтамперная характеристика дуги в структурной схеме рис. 4 представлена в виде знаковой функции uд=Uд∙sign(iд) [5], т.е. принимается, что напряжение на дуге u_д не зависит от тока. Это допущение не должно внести больших погрешностей в результаты исследований, поскольку реальная вольтамперная характеристика закрытой дуги в РТП мало зависит от тока. Зависимость напряжения на дуге от длины дуги uд (lд ) учитывается при экспериментах путем сдвига вольтамперной характеристики вдоль оси ординат. Схема рис. 4 использовалась в дальнейших исследованиях.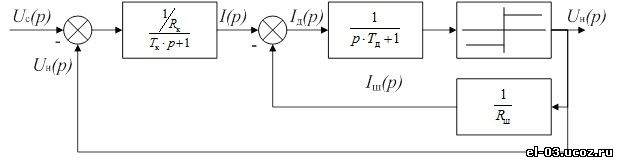 Рис. 4. Структурная схема фазы печи Рис. 4. Структурная схема фазы печи
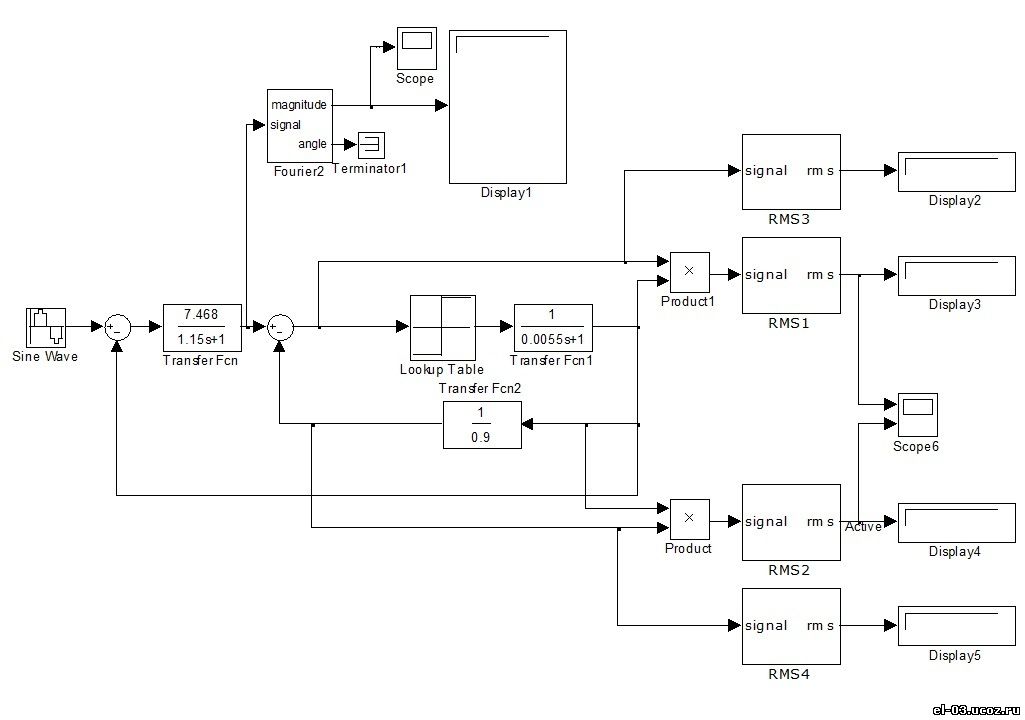 Рис. 5. Схема модели фазы печи в пакете Matlab Simulink Рис. 5. Схема модели фазы печи в пакете Matlab Simulink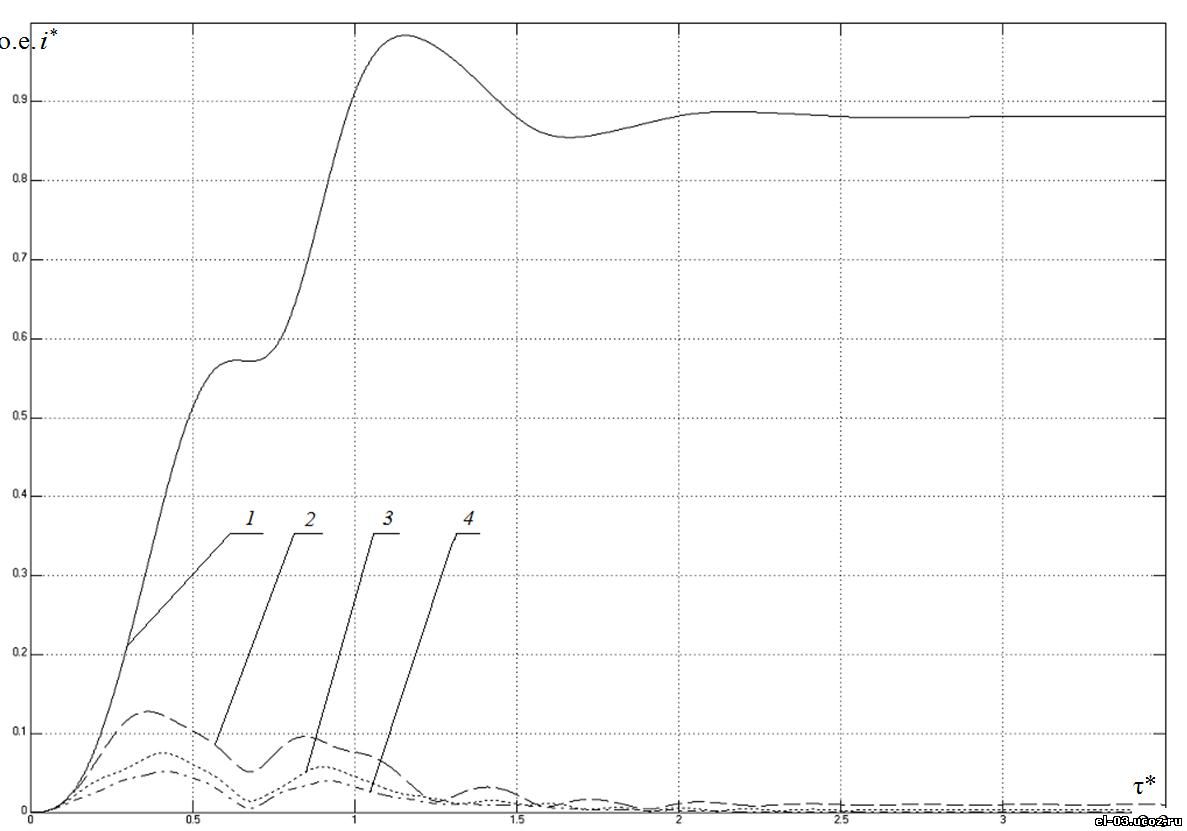 Рис. 6. Временные зависимости амплитудных значений гармонических составляющих фазного тока: 1 – первой гармоники; 2 – третьей гармоники, 3 – пятой гармоники; 4 – седьмой гармоники Рис. 6. Временные зависимости амплитудных значений гармонических составляющих фазного тока: 1 – первой гармоники; 2 – третьей гармоники, 3 – пятой гармоники; 4 – седьмой гармоники
На первом этапе исследования было принято решение из всего многообразия РТП выделить установки для получения ферросилиция, поскольку печи данного типа на сегодняшний день наиболее распространены в промышленности (около 60% всех применяемых РТП). Как показал анализ [6], параметры короткой сети изменяются в ограниченных пределах, что позволяет распространить результаты исследований на весь класс печей. В качестве объекта исследования данной статьи была принята ферросплавная печь типа РКО-16,5, параметры которой приведены в табл. 1. Сопротивление ванны печи, включающее в себя сопротивления твердой шихты стенок тигля и плазмы электрической дуги, примем равным Rв=1,038 мОм [7].Таблица 1. Параметры ферросплавной печи РКО-16,5.
| Параметр | Значение | | Параметры короткой сети | | Реактивные сопротивления | Трансформатор, мОм
| 0,121 | | Короткая сеть, мОм | 0,453 | | Электроды и ванна, мОм | 0,416 | | Печная установка на фазу Xк, мОм | 0,990 | | Активные сопротивления | | Трансформатор, мОм | 0,027 | Короткая сеть, мОм
| 0,043 | | Переходные сопротивления, контактная плита-электрод, мОм | 0,027 | Электрод, мОм
| 0,042 | Печная установка на фазу Rк, мОм
| 0,139 | Электрические характеристики
| Установленная мощность трансформатора, МВА
| 16,5 | Рабочий ток в электроде Iраб, кА
| 63,0 | Рабочее напряжение Uраб, В
| 175,0 | Частота питающей сети f, Гц
| 50 |
Моделирование системы проводилось в относительных величинах для получения универсальных зависимостей, инвариантных к типу печи. При этом за базовые принимались следующие величины:- Базовое время tб – время равное периоду частоты питающего напряжения tб=0,02 с;
- Базовое напряжение Uб – рабочее напряжение печи: Uб=175,0 В;
- Базовый ток Iб – рабочий ток в электроде печи: Iб=63000 А;
- Базовое сопротивление Rб – сопротивление ванны печи: Rб=1,038 мОм.
Тогда относительные величины могут быть определены как:
- Относительное время: т*=t/tб;
- Относительная постоянная времени короткой сети и трансформатора: Tк*=Tк/tб;
- Относительная постоянная времени дуги: Tд*=Tд/tб;
- Относительная круговая частота: f*=2*pi*f*tб;
- Относительное напряжение: u*=u/Uб;
- Относительный ток: i*=i/Iб;
- Относительное активное сопротивление короткой сети и трансформатора: rк*=R/Rб;
- Относительное сопротивление дуги: rд*=Rд/Rб;
- Относительное сопротивление шихты: rш*=Rш/Rб.
Проведение эксперимента и анализ полученных результатов
Особенностью системы управления РТП является работа в режиме поддержания фазных токов путем регулирования длины дуги и напряжения на вторичной обмотке трансформатора. Поэтому в процессе исследования для выполнения этого условия при варьировании напряжения на дуге (длины дуги) и сопротивления шихты сохранялось практически неизменным значение полного фазного тока I=const.
При проведении эксперимента на модели выделялись первая, третья, пятая, седьмая, девятая и одиннадцатая гармонические составляющие фазного тока, поскольку значения четных гармонических составляющих исследуемого тока незначительны и близки к нулю.
В процессе моделирования исследовалось влияние сопротивления дуги rд* (длины дуги) и сопротивления шихты rш* (тигля) на гармонический состав суммарного фазного тока печи i*, на величины токов, протекающих по дуге iд* и по шихте iш*, одновременно рассчитывались: полная мощность печи p*, определяемая как p*=pд*+pш*, мощность, выделяемая в дуге pд*=iд*•uд*, и мощность, выделяемая в шихте pш*=iд*^2*rш*. На рис. 7 приведены рассчитанные на модели зависимости амплитуды третьей гармоники полного тока i* (рис. 7 а)), полной мощности p*, мощности в шихте pш* и мощности в дуге pд* (рис. 7 б)) от отношения токов (iш*)/(iд*) при относительном сопротивлении шихты rш*=0,5 и изменении напряжения в дуги uд* от 0,2 до 0,9.
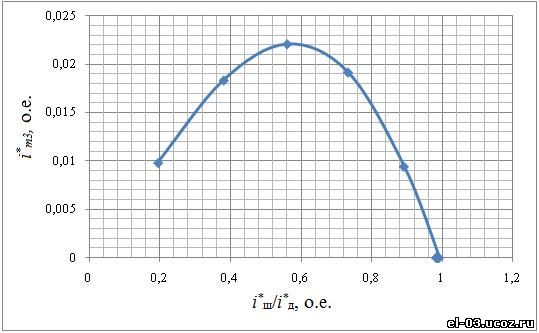 а) а)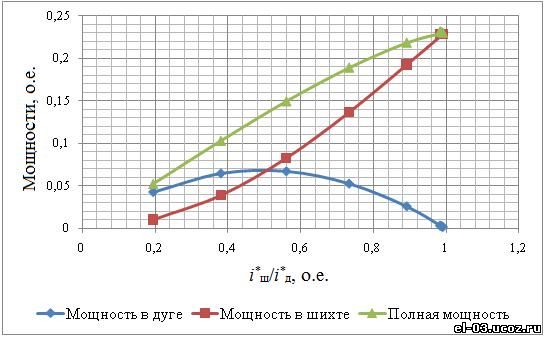 б) б)Рис. 7. Зависимости амплитуды третей гармоники, полной мощности, мощности в дуге и мощности в шихте от отношения токов
Для доказательства адекватности разработанной модели, снятые величины сравнивались с экспериментальными данными, полученными на действующих печах ДСП-100Н3А [4], ДСП-10 и ДСП-25 [8]. В частности, для оценки адекватности разработанной модели рассчитывались значения мощностей p* и pд* для открытой дуги, что соответствует rш*=inf. Совпадение результатов расчета на модели с литературными данными свидетельствует об адекватности разработанной модели. Наличие незначительных расхождений в значениях обусловлено погрешностями вычислительного эксперимента, а также принятыми в процессе моделирования допущениями.
Анализируя полученные данные, следует отметить, что изменение сопротивления шихты оказывает малое влияние на гармонический состав тока. Это обстоятельство объясняется тем, что искажение тока вызвано в основном нелинейностью сопротивления дуги, а не сопротивлением шихты (которое в рассматриваемом случае было принято чисто активным).
В то же время соотношение токов, протекающих по шихте iш* и дуге iд*, оказывает значительное влияние на изменение высших гармонических составляющих тока, в частности, третьей гармонической составляющей, зависимость которой от соотношения токов приведена на рис. 7 а). Как следует из сопоставления зависимостей, приведенных на рис. 7 а) и б), амплитуда третьей гармоники тока im3* изменяется с im3*=0,01 до im3*=0,022, т.е. практически в 2 раза, при изменении тока дуги в диапазоне 0,1<=iд*<=0,4. При этом изменяется как полная мощность p*, выделяемая в печи, так и соотношения составляющих полной мощности pд* и pш*. Проведенный анализ показывает, что между гармоническим составом фазного тока РТП с закрытой дугой и распределением мощностей в ванне печи имеется явно выраженная зависимость, которая может быть использована для идентификации теплового режима в печи.
Определение желаемого соотношения мощностей, выделяемых в дуге и в шихте РТП и, следовательно, значения измеряемой высшей гармоники, которое можно поддерживать в процессе плавки, выходит за рамки данной статьи, поскольку требует решения более сложной тепловой задачи. Тем не менее, проведенные исследования показывают, что анализ гармонического состава кривой фазного тока РТП с закрытой дугой позволяет оценивать распределение мощностей в зоне плавления.
Выводы
- Показана возможность идентификации составляющих мощностей, выделяемых в дуге и в шихте в РТП по контролю гармонического состава кривой фазного тока.
- Разработанная модель позволяет рассчитать зависимости высших гармонических составляющих тока, мощностей, выделяемых в шихте и в дуге, а также полные мощности, выделяемые в печи от времени, полного тока или отношения токов, протекающих в дуге и в шихте. Эти зависимости могут быть использованы как для анализа распределения мощностей в печи, так и для изменения режима работы печи.
- Полученные зависимости могут быть использованы в дальнейшем для обоснования критерия желаемого распределения мощностей и построения системы управления тепловым режимом.
Список литературы
- Воскобойников В. Г., Кудрин В. А., Якушев А. М. Общая металлургия: учебник для вузов. – М. : ИКЦ «Академкнига», 2005.
- Электрические промышленные печи. Дуговые печи и установки специального нагрева. / под ред. А.Д. Свенчанского. – М. : Энергоиздат, 1981.
- Свенчанский А.Д., Гуттерман К.Д. Автоматическое регулирование электрических печей. – М. : Энергия, 1965.
- Гордиенко В.А., Дрогин В.И., Попов А.Н., Пирогов Н.А. Расчет и измерение напряжения дуги в ДСП. Математическое моделирование и расчет дуговых и плазменных сталеплавильных печей. Сборник научных трудов ВНИИЭТО. – М.: Энергоатомиздат, 1983 с.
- Хаинсон А.В. О точности расчета электрической цепи ДСП. Математическое моделирование и расчет дуговых и плазменных сталеплавильных печей. Сборник научных трудов ВНИИЭТО. – М.: Энергоатомиздат, 1983.
- Короткие сети и электрические параметры дуговых печей. Справочник. / под ред. Я.Б. Данциса и Г.М. Жилова – М.: Металлургия, 1987.
- Кулинич В.И., Головачев Н.П., Клименко В.Ф., Католивцев В.И., Варкентин П.П.. Параметры, определяющие производительность электропечных установок // Сталь. – 2002. – №5. – С. 30-34.
- Минеев Р. В., Михеев А.П. Электродинамика дуговых сталеплавильных печей в задачах оптимизации электроснабжения. Современное состояние электропечестроения (по материалам VII международного конгресса по электротермии). Дуговой нагрев и новые виды нагрева. – М.: 1975.
|
| Категория: Статьи | Добавил: DEADalus (20.06.2011)
|
| Просмотров: 3578
| Рейтинг: 0.0/0 |
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] | |
 | |  |
|
| Статистика |

Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
|






